Category: Uncategorised

Do you ever worry about how you declare NUMERIC or DECIMAL data types in SQL?
Do you sometimes “add a bit more” precision—just to be safe?
Have you considered how that small decision could actually change your arithmetic results?

I ran into this recently when comparing data between two environments that should have produced identical results. One calculated field was slightly off — and the culprit turned out to be a difference in numeric data type declarations.

It’s essentially a rounding problem, but one that happens implicitly during calculations. That makes it harder to detect and can lead to significant discrepancies when aggregating results (think invoices or financial reporting).

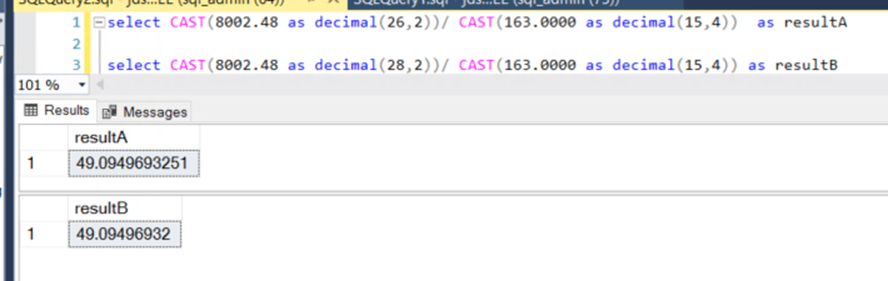
The only difference was the declaration of the value on line 1 as DECIMAL(26,2) versus DECIMAL(28,2) on line 3.

Both store two decimal places — but result B allowed two extra digits of precision. That’s fine when storing or comparing raw values, but once those numbers are used in arithmetic operations, small differences can creep in. Summed over hundreds of thousands of rows, those differences become noticeable and potentially misleading.

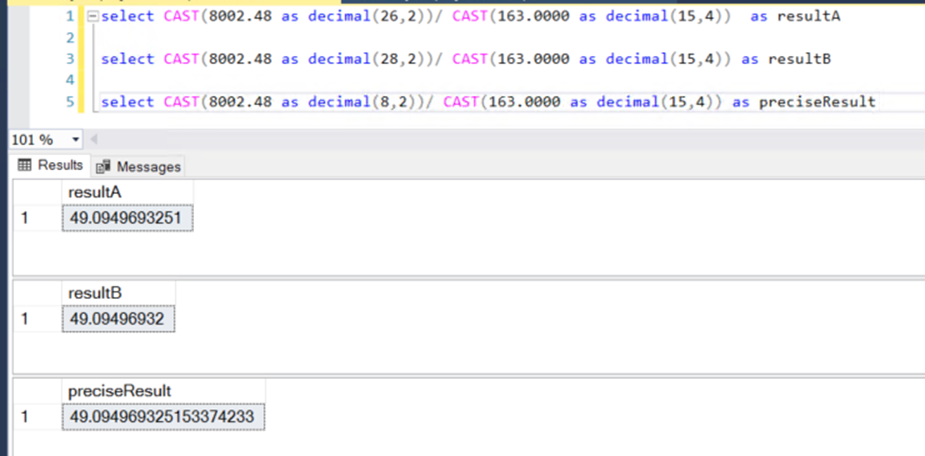
If we increase the number of visible decimal places, we can actually see the precision difference.

So, what’s happening between Result A and Result B?

Every time SQL performs an arithmetic operation, it must determine the data type of the result. The rules differ depending on the operation — addition, subtraction, multiplication, or division.

How SQL Server Determines Result Precision

🔗 Precision, scale, and length (Transact-SQL)

For division, SQL Server uses the following formula:

Precision = p1 - s1 + s2 + max(6, s1 + p2 + 1)

Scale = max(6, s1 + p2 + 1)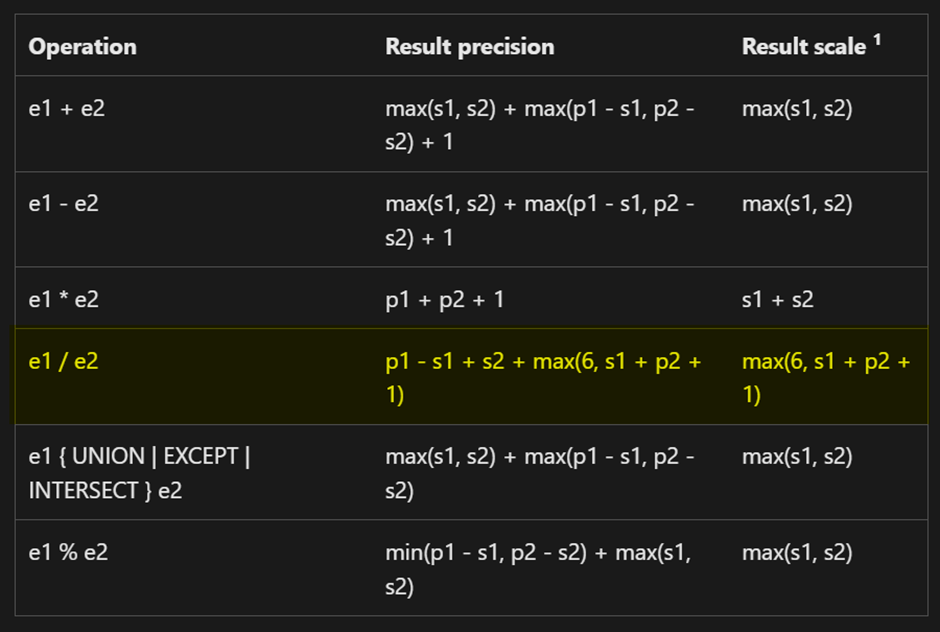

In our case:

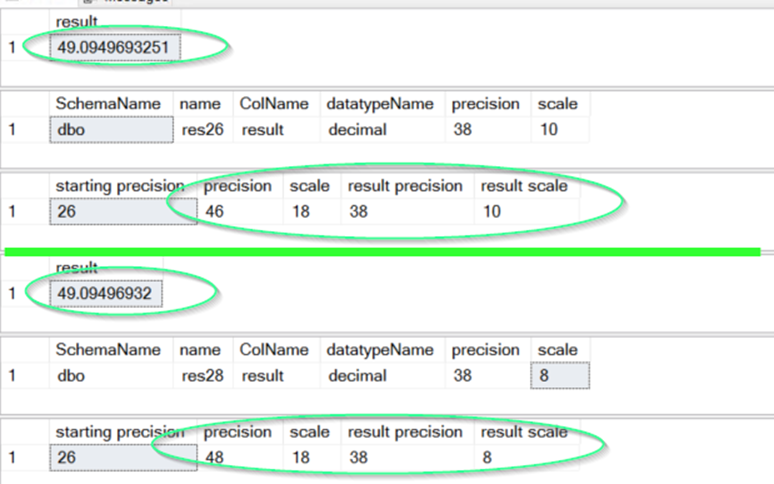
Precision = 28 - 2 + 4 + max(6, 2 + 15 + 1) = 48
Scale = max(6, 2 + 15 + 1) = 18

However, there’s a second step — the result precision cannot exceed 38.

If it does, SQL Server adjusts it using this rule:

Scale cannot be greater than 38 - (precision - scale)

So in this example:

38 - (48 - 18) = 8

This truncation explains the observed rounding difference between the two environments.

Takeaway

Be mindful when declaring your numeric precision and scale. “Just adding a few more digits” can cause unintended changes in how SQL Server performs arithmetic — and those small differences can scale up quickly in production data.

Here is a script if you want to test it or check it yourself:

DROP TABLE IF EXISTS res26, res28

select TOP 1 CAST(8002.48 as decimal(26,2))/ CAST(163.0000 as decimal(15,4))  as result
INTO dbo.res26
from sys.objects 
  
select TOP 1 CAST(8002.48 as decimal(28,2))/ CAST(163.0000 as decimal(15,4)) as result
INTO dbo.res28
from sys.objects 


select * from dbo.res26
SELECT schema_name(o.schema_id) as SchemaName,
       o.name,
       c.name as ColName,
       t.name as datatypeName,
       c.precision,
       c.scale
  FROM sys.objects     o
  JOIN sys.all_columns c ON o.object_id = c.object_id
  JOIN sys.types       t ON c.user_type_id = t.user_type_id
  where schema_name(o.schema_id) = 'dbo'
    and o.name = 'res26'

DECLARE @p1 tinyint = 26
       ,@s1 tinyint = 2
       ,@p2 tinyint = 15
       ,@s2 tinyint = 4
       ,@precision tinyint 
       ,@scale     tinyint

SELECT @precision =  @p1 - @s1 + 4 + GREATEST(6, @s1 + @p2 + 1),
       @scale = GREATEST(6, @s1 + @p2 +1)
   
SELECT 'starting precision' = '26',
       'precision' = @precision,
       'scale'     = @scale,
       'result precision' = IIF(@precision > 38, 38, @precision),
       'result scale' = LEAST(@scale, 38 - (@precision - @scale))

GO 

select * from dbo.res28

SELECT schema_name(o.schema_id) as SchemaName,
       o.name,
       c.name as ColName,
       t.name as datatypeName,
       c.precision,
       c.scale
  FROM sys.objects     o
  JOIN sys.all_columns c ON o.object_id = c.object_id
  JOIN sys.types       t ON c.user_type_id = t.user_type_id
  where schema_name(o.schema_id) = 'dbo'
    and o.name = 'res28'


DECLARE @p1 tinyint = 28
       ,@s1 tinyint = 2
       ,@p2 tinyint = 15
       ,@s2 tinyint = 4
       ,@precision tinyint 
       ,@scale     tinyint

SELECT @precision =  @p1 - @s1 + 4 + GREATEST(6, @s1 + @p2 + 1),
       @scale = GREATEST(6, @s1 + @p2 +1)
   
SELECT 'starting precision' = '26',
       'precision' = @precision,
       'scale'     = @scale,
       'result precision' = IIF(@precision > 38, 38, @precision),
       'result scale' = LEAST(@scale, 38 - (@precision - @scale))